
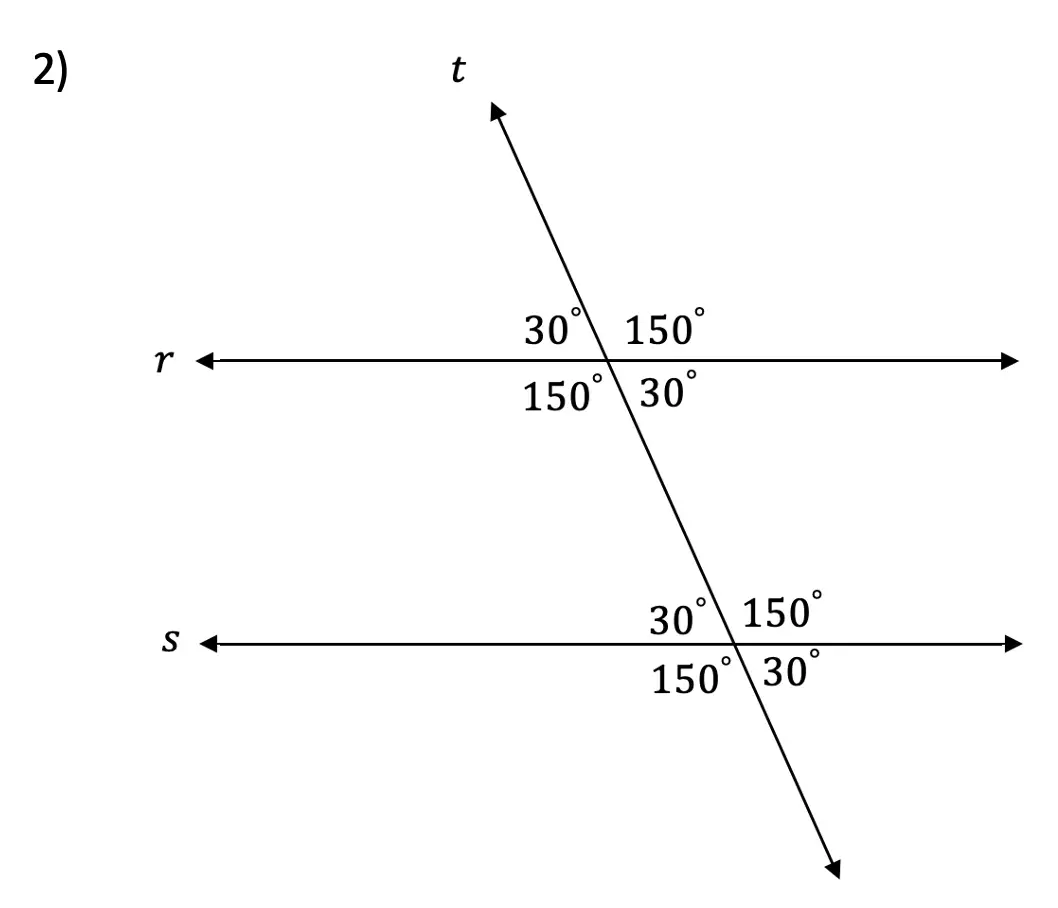
If you found the three questions at the beginning of this article challenging, then take another look at them before reading the solutions below. It may that this refresher cleared up a few things for you. There are all kinds of fancy geometry names these angles had back in high school geometry - for example, angles 3 and 6 are “alternate interior angles” (does that bring back pre-prom memories?) - but for the purpose of the GMAT, you don’t need to know any terms more technical than “big angles” and “small angles.” Keep it simple.
#Parallel angles plus
Any big angle plus any small angle equals 180° Notice that we could divide these eight angles into “big” angles (angles 1 & 4 & 5 & 8) and “small” angles (angles 2 & 3 & 6 & 7). OK, if we are guaranteed that the lines are parallel, and another line intersects these parallel lines, what do we know? This diagram summarizes everything you will need to know. You have to see, printed in black & white: the lines are parallel.
Two lines that look parallel could be half a degree off from being truly parallel - that difference would not be visually apparent, but none of the special parallel-line facts would be true if the two lines are not exactly parallel. BUT, if two lines look parallel, you can’t assume they are parallel. Unless otherwise specified, all diagrams on the GMAT Problem Solving are drawn as accurately as possible. This has an important implication for diagrams. Almost parallel is absolutely worthless in geometry. Important idea #1 in this context is: while there are a number of special geometry facts that are true for parallel lines, absolutely none of them are true for lines that are almost parallel. That’s a triangle with three right angles!!) Consider a triangle formed by three points: (1) the North Pole, (2) the intersection of the Prime Meridian and the Equator, and (3) the intersection of the 90° West meridian and the Equator. Consider the surface of the Earth, which is approximately spherical. ( Cool fact that is 110% irrelevant to the GMAT: in some alternate, non-Euclidean geometries, there are no parallel lines possible, and in these geometries, the 180°-Triangle Theorem does not hold. A more dramatic way to say this would be: God Himself would not be able to create a triangle in the plane the sum of whose angles is not 180°. This is a fact true, not just for certain triangles, but for every possible triangle. The sum of all three angles in any triangle equals 180°. The special properties of parallel lines are also directly connected to one of the most famous theorems in Geometry, the 180°-Triangle Theorem: These facts include what angles are equal, and which angles have other mathematical relationships, if the lines are parallel. Some of the most fundamental geometry facts have to do with the special properties of parallel lines. Solutions will come at the end of this article.


 0 kommentar(er)
0 kommentar(er)
